Question

Which statement describes the function y=ax^n when a=1 and n is odd?

A. The graph opens down.
B. The graph is symmetric about the origin
C.The graph does not pass through the origin
D. The graph has more than one x intercept

Answer 1

ANSWER

B. The graph is symmetric about the origin

EXPLANATION.

The given function is


`y = a {x}^(n)`

When a=1,


`y = {x}^(n)`

Let,


`f(x)= {x}^(n)`


`f(-x)= {( - x)}^(n)`

Since n is odd,


`f(-x)=-{( x)}^(n)`


`\Rightarrow f(-x)=-f(x)`

This implies that, the function


`y={x}^(n)`

is symmetric with respect to origin.

The correct answer is B

Answer 2

B. The graph is symmetric about the origin

Explanation:

We have the function
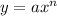`y=a x^(n)`, where a= 1 and n= odd.

'Leading Coefficient Test' states that 'when 'n' is odd and the leading coefficient is positive, then the graph falls to the left and rises to the right'.

As we have,
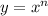`y=x^(n)`, where n is odd and leading coefficient a=1.

So, the graph of this function will fall to the left and rise to the right.

Then, option A is not correct.

Moreover, x= 0 ⇒
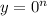`y=0^(n)` ⇒ y= 0.

So, this function passes though (0,0) i.e. origin.

Then, option C is not correct.

Also, 'x-intercept is the point when graph cuts the x-axis i.e. when y= 0'.

So, we have,

`0=x^(n)` ⇒ x= 0.

Thus, the only x-intercept is the point (0,0).

Then, option D is not correct.

From the graph below, we see that, the graph of
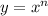`y=x^(n)` is symmetric about origin.

Hence, option B is correct.