Question

Use the alternative form of the derivative to find the derivative at x = c (if it exists). (If the derivative does not exist at c, enter UNDEFINED.) h(x) = |x + 8|, c = -8

Answer 1

The derivative of the function does not exist.

Explanation:

The alternative form of a derivative is given by:

`f'(c)= \lim_(x \to c) (f(x)-f(c))/(x-c)`

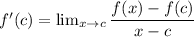
Our function is defined as:

h(x)=|x+8|

i.e. h(x)= -(x+8) when x+8<0

and x+8 when x+8≥0

i.e. h(x)= -x-8 when x<-8

and x+8 when x≥-8

Hence now we find the derivative of the function at c=-8

i.e. we need to find the Left hand derivative (L.H.D.) and Right hand derivative (R.H.D) of the function.

The L.H.D at a point 'a' is calculated as:

`\lim_(x \to a^-) (f(x)-f(a))/(x-a)\\\\=\lim_(h \to0) (f(a-h)-f(a))/(a-h-a)= \lim_(h\to 0)  (f(a-h)-f(a))/(-h)`

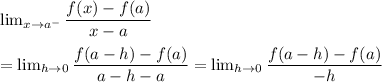
Similarly R.H.D is given by:

`\lim_(x \to a^+) (f(x)-f(a))/(x+a)\\\\=\lim_(h \to 0) (f(a+h)-f(a))/(a+h-a)= \lim_(h\to 0) (f(a+h)-f(a))/(h)`

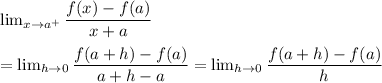
Now for L.H.D we have to use the function h(x) =-x-8

and for R.H.D. we have to use the function h(x)=x+8

L.H.D.

we have a=-8

`\lim_(x \to (-8)^-) (h(x)-h(-8))/(x-(-8))\\\\= \lim_(h \to0) (h(-8-h)-h(-8))/(-8-h-(-8))= \lim_(h\to 0) (h(-8-h)-h(-8))/(-h)`

=
`\lim_(h \to 0) (8+h-8-0)/(-h)= \lim_(h \to 0)(h)/(-h)=-1`

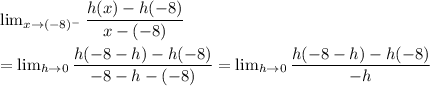
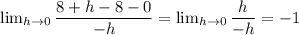
similarly for R.H.D.

`\lim_(x \to (-8)^+) (h(x)-h(-8))/(x-(-8))\\\\=\lim_(h \to 0) (h(-8+h)-h(-8))/(-8+h-(-8))= \lim_(h\to 0) (h(-8+h)-h(-8))/(h)`

`\lim_(h \to 0) (-8+h+8-0)/(h)=\lim_(h \to 0)(h)/(h)=1`

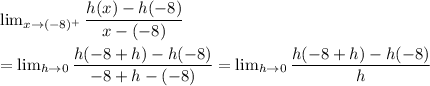
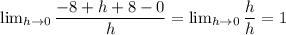
Now as L.H.D≠R.H.D.

Hence, the function is not differentiable.