Answer:
The given statement is true.
Explanation:
We are asked whether the following statement is true or not:
(0.72) to the 7th power > (-7.2) to the 7th power
This statement is true since the value of
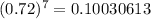
Also the value of the exponent
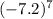 will be negative as odd power of a negative number is always negative.
will be negative as odd power of a negative number is always negative.
Also

and we know that any positive number is always greater than negative number.
Hence,
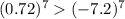
Hence, the following statement is true.