Question

Use the ratio test to determine whether the series is convergent or divergent.

Answer 1

Option B is correct, i.e. Divergent series.

Explanation:

Given the series is:-

(2/1²) + (4/2²) + (8/3²) + (16/4²) +.....

n-th term of the series would be:- aₙ = (2ⁿ)/(n²)

(n+1)-th term of the series would be:- aₙ₊₁ = (2ⁿ⁺¹)/(n+1)²

Using Ratio test:-

`L = \lim_(n \to \infty) |(a_(n+1))/(a_(n))|\\L = \lim_(n \to \infty) |((2^(n+1))/(n+1)^2)/((2^n)/(n^2))|\\L = \lim_(n \to \infty) |(2*n^2)/((n+1)^2)|\\L = \lim_(n \to \infty) |(2)/((1 + 1/n)^2)|\\L = |(2)/((1 + 1/\infty)^2)|\\L = |(2)/((1 + 0)^2)|\\L = 2`

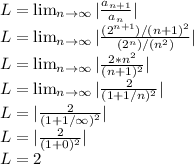
If L > 1, then series is divergent.

Since we got L = 2 and 2 > 1. It means given series is divergent.

Hence, option B is correct, i.e. Divergent series.

Answer 2

Divergent

Explanation:

Given series has general term as

`(2^n)/(n^2)`

n+1 th term =
`(2^(n+1))/((n+1)^2)`

WE have to check whether this series converges or diverges

Let us use ratio test

Ratio of n+1 th term to nth term

=
`(2n^2)/((n+1)^2) =(2)/((1+(1)/(n) )^2`

by dividing numerator and denominator by n square

Take limits as n tends to infinity

The ratio tends to 2

Since ratio >2, the series diverges