Question

What is the expression for f(x) when we rewrite
(5⁻⁴ˣ⁺⁷)÷(125x) as 5^f(x)

Answer 1

Answer: The answer is f(x) = -7x + 7.

Step-by-step explanation: We are give a relation as follows :

`5^(-4x+7)/ 125^x=5^(f(x)).`

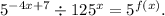
From here, we need to find the expression for f(x).

Here, we will be using the following properties of exponents :

`(i)~(a^x)/(a^y)=a^(x-y).\\\\(ii)~a^x=a^y~\Rightarrow x=y.`

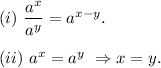
We have

`5^(-4x+7)/ 125^x=5^(f(x))\\\\\Rightarrow5^(-4x+7)/ 5^(3x)=5^(f(x))\\\\\\\Rightarrow (5^(-4x+7))/(5^(3x))=5^(f(x))\\\\\\\Rightarrow 5^(-4x+7-3x)=5^(f(x))}\\\\\Rightarrow 5^(-7x+7)=5^(f(x))\\\\\Rightarrow -7x+7=f(x).`

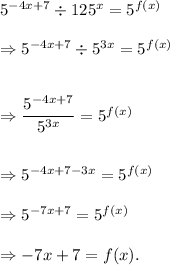
Thus, the required expression is f(x) = -7x + 7.