Answer: The answer is f(x) = -7x + 7.
Step-by-step explanation: We are give a relation as follows :
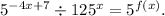
From here, we need to find the expression for f(x).
Here, we will be using the following properties of exponents :
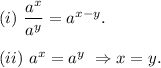
We have

Thus, the required expression is f(x) = -7x + 7.