Question

If f(x) = 1 – x, which value is equivalent to |f(i)|?

Answer 1

Option C is correct

`√(2)` value is equivalent to |f(i)|

Explanation:

Modulus of the complex number z = a+ib is given by:

`|z| = √(a^2+b^2)`

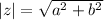
As per the statement:

Given the function:

`f(x) = 1-x`

Substitute x = i we have;

`f(i) = 1-i`; where, i is the imaginary part.

We have to find |f(i)|.

`|f(i)| = |1-i|`

By definition of modulus;

`|f(i)| =√(1^2+(-1)^2)`

⇒
`|f(i)| =√(1+1)`

⇒
`|f(i)| =√(2)`

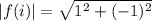
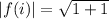
Therefore, the value of |f(i)| is,
`√(2)`

Answer 2

Option 3

Explanation:

We are given that

f(x) = 1-x

To find out f(i) we replace x by i

f(i) = 1-i

Thus this is a complex number with real part = 1 and imaginary part =-1

Modulus of f(i) = |1-i| =

`√(1^2+(-1)^2) \\=√(2)`

Thus answer is option C

square root of 2