Answer: The answer is both are same.
Step-by-step explanation: We are given to describe the relationship between the domain of an inverse sine function and the range of a sine function.
Let
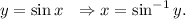
We know from Trigonometry that the domain and range of sine function are

Also, the domain and range of inverse sine function is given by

See the attached figures for more understanding.
Thus, it is clear from the explanation that the range of sine function and the domain of inverse sine function are same and it is equal to [-1, 1]