Answer:
Probability that the spinner will stop on an odd number or a multiple of 5 is 0.6
Explanation:
Probability =
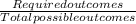
We are given the equal regions numbered from 1 through 20 which means that our total possible outcomes are 20
Total possible outcomes: 20
Outcomes that spinner will stop on an odd number, n(Odd): 10
1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Probability of spinner stoping on Odd number:
P(Odd) =
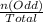 =
=
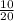 =
=
 = 0.5
= 0.5
Outcomes that spinner will stop on a multiple of 5, n(5): 4
5, 10, 15, 20
Probability of spinner stoping on multiple of 5:
P(5) =
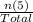 =
=
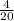 =
=
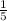 = 0.2
= 0.2
Odd numbers which are a multiple of 5 are: 5 and 15
So,
P(Odd and 5) =
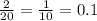
Thus Probability of spinner stopping at odd number or a multiple of 5 becomes:
P(Odd or 5) = P(Odd) + P(5) - P(Odd and 5) = 0.5 + 0.2 - 0.1 = 0.6