Question

Two points have the coordinates P (6, -3,9) and Q (3, -6, -3). A point R divides line PQ internally in the ratio 1:2. The position vectors of P, Q and Rare p, q and r respectively.

(a) Express the position vector of p and q.
i. In terms of p and q.
ii. In terms of i, j and k
(b) Hence state the coordinates of R.

Answer 1

(a) i. See comment...

(a) ii. We have

`\vec p = 6\,\vec\imath - 3\,\vec\jmath + 9\,\vec k`

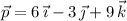
and

`\vec q = 3\,\vec\imath - 6\,\vec\jmath - 3\,\vec k`

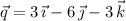
(b) We can parameterize the line segment from P to Q by the vector function

`\vec r(t) = (1-t) \vec p + t \vec q = (6-3t) \, \vec\imath + (-3-3t) \,\vec\jmath + (9-6t) \,\vec k`

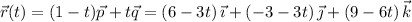
with
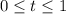`0\le t\le1`. The point R is located 1/3 of the way along this line segment, i.e. at
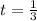`t=\frac13`, so its position vector is

`\vec r\left(\frac13\right) = 5\,\vec\imath -4\,\vec\jmath + 7\,\vec k`

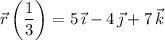
and hence its coordinates are
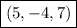`\boxed{(5,-4,7)}`.