Question

Taylor graphs the system below on her graphing calculator and decides that f(x)=g(x) at x=0, x=1, and x=3. Provide Taylor some feedback that explains which part of her answer is incorrect and why it is incorrect. f(x)=2x+1

g(x)=2x^2+1

Answer 1

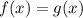`f(x)=g(x)` at x= 0 and x= 1 and not at x= 3.

Explanation:

We have the functions,
`f(x)=2x+1` and
`g(x)=2x^2+1`.

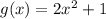It is given that,

At x=0, x=1, and x=3,
`f(x)=g(x)`

i.e.
`2x+1=2x^2+1`

i.e.
`2x^2-2x=0`

i.e.
`2x(x-1)=0`

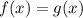
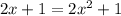
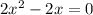
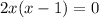
i.e. x= 0 and (x-1)= 0

i.e. x= 0 and x= 1.

Also, after plotting the graphs of both the functions, we see their intersection point are (0,1) and (1,3).

Thus, we get that
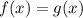`f(x)=g(x)` at x= 0 and x= 1 and not at x= 3.