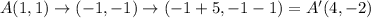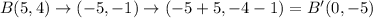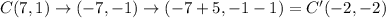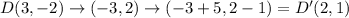Question

A parallelogram has coordinates A(1, 1), B(5, 4), C(7, 1), and D(3, -2). What are the coordinates of parallelogram A′B′C′D′ after a 180° rotation about the origin and a translation 5 units to the right and 1 unit down?

Answer 1

`A'(4,-2)`
`B'(0,-5)`
`C'(-2,-2)`
`D'(2,1)`

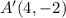
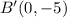
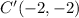
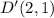
Explanation:

The given parallelogram has coordinates A(1, 1), B(5, 4), C(7, 1), and D(3, -2).

The rotation of
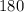`180\degree`about the origin has the mapping;

`P(x,y)\rightarrow P'(-x,-y)`

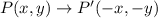
This implies that;

`A(1,1)\rightarrow (-1,-1)`

`B(5,4)\rightarrow (-5,-4)`

`C(7,1)\rightarrow (-7,-1)`

`D(3,-2)\rightarrow (-3,2)`

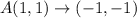
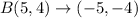
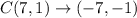
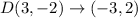
A translation of 5 units to the right and 1 unit down has the mapping;

`P(x,y)\rightarrow P'(x+5,y-1)`

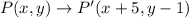
We apply this to the resulting coordinates to obtain;

`A(1,1)\rightarrow (-1,-1) \rightarrow (-1+5,-1-1)=A'(4,-2)`

`B(5,4)\rightarrow (-5,-1) \rightarrow (-5+5,-4-1)=B'(0,-5)`

`C(7,1)\rightarrow (-7,-1)\rightarrow (-7+5,-1-1)=C'(-2,-2)`

`D(3,-2)\rightarrow (-3,2)\rightarrow (-3+5,2-1)=D'(2,1)`