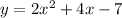Question

Write a quadratic function, in standard form, that fits the set of points. Solve it as a system of three equations. (-4, 9), (0, -7), and (1, -1)

Answer 1

`\boxed{y=2x^2+4x-7}`

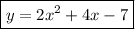
Explanation:

Let the quadratic function be

`y=ax^2+bx+c`

We substitute
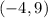`(-4,9)` into the equation to obtain;

`9=a(-4)^2+b(-4)+c`

`\Rightarrow 9=16a-4b+c---(1)`

We substitute
`(0,-7)` to obtain;

`-7=a(0)^2+b(0)^2+c`

`\Rightarrow c=-7---(2)`

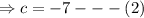
We finally substitute
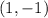`(1,-1)` to obtain;

`-1=a(1)^2+b(1)^2+c`

`\Rightarrow -1=a+b+c---(3)`

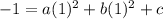
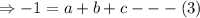
We put equation (2) into equation (1) to get;

`9=16a-4b-7`

`16a-4b=16`

`\Rightarrow 4a-b=4---(4)`

`\Rightarrow -1=a+b-7`

`\Rightarrow a+b=6---(5)`

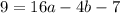
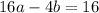
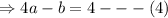
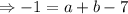
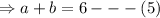
We add equation (4) and (5) to get;

`4a+a=6+4`

`\Rightarrow 5a=10`

`\Rightarrow a=2`

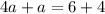
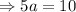
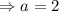
We put
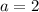`a=2` into equation (5) to get;

`2+b=6`

`\Rightarrow b=6-2`

`\Rightarrow b=4`

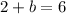
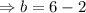
The reqiured quadratic function is

`y=2x^2+4x-7`