2 Answers

Saus · Answer 1 · 2023-09-30T13:05:37+0000

Answer:

A system of two linear equations can have one solution, an infinite number of solutions, or no solution.

===================================================

Step-by-step explanation:

An equation is something like
$\text{y} = 2\text{x}+5$ and
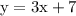
$\text{y} = 3\text{x}+7$

When we combine two such equations to form a group (of sorts), we consider this to be a system of equations.

We use a single curly brace to write the system

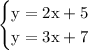
$\begin{cases}\text{y} = 2\text{x}+5\\\text{y} = 3\text{x}+7\end{cases}$

Here are the three cases mentioned when it comes to solutions.

If the two lines intersect at exactly one point, then the system has exactly one solution. This system is consistent and independent.
If the two lines are the same, they intersect at infinitely many points along that line. One line perfectly overlaps the other. Therefore, this scenario leads to infinitely many solutions. The system is dependent because one line depends on the other (since they are one in the same). This system is also consistent because it has at least one solution.
Lastly, if the two lines are parallel, then they never cross. The lack of crossing points means there aren't any solutions. We call this an inconsistent system.

Side note: Any solution is of the form (x,y)

Please log in or register to add a comment.