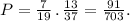Question

There are chocolates in a box, all identically shaped. There are 8 filled with nuts, 16 with caramel, and 14 are solid chocolate. You randomly select one piece, eat it, and then select a second piece. Find the probability of selecting 2 solid chocolates in a row.

Answer 1

P =
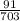`(91)/(703)` ≅ 12.95%.

Explanation:

The total amount of chocolates in the box is 8 + 16 + 14 = 38, 14 of which are solid.

Let's calculate the probability of getting a solid chocolate in the first selection:

`P(1S) = (14)/(38) = (7)/(19).`

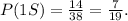
Given that the first piece was solid, there are now 37 pieces of chocolate in the box, 13 of which are solid. Let's now calculate the probability of selecting another solid chocolate:

`P(2S\,|\,1S) = (13)/(37).`

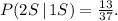
Thus, the probability of selecting two solid chocolates in a row is the product of the two probabilities calculated above:

`P = (7)/(19)\,.\,(13)/(37) = (91)/(703).`