Answer:
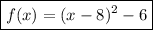
Explanation:
The graph in the attachment is a quadratic function whose vertex is in the fourth quadrant.
The coordinates of a point in the fourth quadrant is of the form
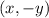
Considering the options, the vertex must have coordinates
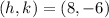 and
and
 .
.
The quadratic function in vertex form is written as;
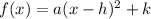
Therefore the equation of the quadratic function is;
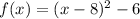
The correct answer is option D