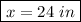Question

98 POINTS!!

1. What is the value of x?
2.What is the value of x?
3.What is the value of x?

Answer 1

Look at the picture.

If ABC is any triangle and AD bisects (cuts in half) the angle BAC, then

`(AB)/(DB)=(AC)/(DC)`

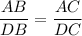
1. In our triangle we have the proportion:

`(AD)/(AC)=(BD)/(BC)`

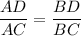
We have

AD = 2.25, AC = 3, BC = 4, BD = x.

Substitute:

`(2.25)/(3)=(x)/(4)`

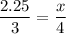
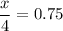`(x)/(4)=0.75` multiply both sides by 4

`\boxed{x=3}`

2. In our triangle we have the proportion:

`(BD)/(BA)=(CD)/(CA)`

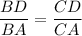
We have

BD = x + 4, BA = 8, CD = 2x + 1, CA = 12.

Substitute:

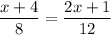`(x+4)/(8)=(2x+1)/(12)` cross multiply

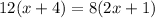`12(x+4)=8(2x+1)` use distributive property a(b + c) = ab + ac

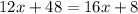`12x+48=16x+8` subtract 48 from both sides

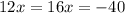`12x=16x=-40` subtract 16x from both sides

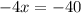`-4x=-40` divide both sides by (-4)

`\boxed{x=10}`

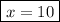
3. We have the similar triangles (AAA). Therefore the lengths of the sides are in proportion:

`(x)/(8)=(15)/(5)`

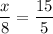
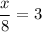`(x)/(8)=3` multiply both sides by 8

`\boxed{x=24\ in}`

Answer 2

1. Set up a ratio: 3/2.25 = 4/x

Cross multiply:

3x = 2.25*4

3x = 9

Divide both sides by 3:

x = 9/3

x = 3

2. Set up a ratio: 12/2x+1 = 8/x+4

Cross multiply:

12(x+4) = 8(2x+1)

Simplify:

12x +48 = 16x +8

Subtract 8 from each side:

12x +40 = 16x

Subtract 12x from each side:

40 = 4x

Divide both sides by 4:

x = 40/4

X = 10

3. Find the ratio of the smaller triangle to the larger triangle: using the two ends: 15 /5 = 3

The larger triangle is 3 times larger than the smaller one.

Because the two given angles are on opposite sides, this means the sides of the triangle are mirrored so X is the equivalent of side 8 times the ratio:

x = 8 *3 = 24