Answer:
3
Explanation:
So we're given:
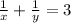 and that:
and that:
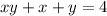 . And now we need to solve for:
. And now we need to solve for:
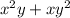 .
.
Original equation:
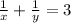
Multiply both sides by xy
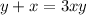
Now take this and plug it as x+y into the second equation:
Original equation:
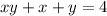
Substitute 3xy as x+y

Combine like terms:
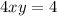
Divide both sides by 4
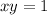
Divide both sides by x:
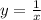
Original equation:
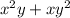
Substitute 1/x as y
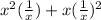
Multiply values:
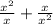
Simplify:
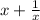
Substitute y as 1/x back into the equation:
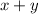
so now we just need to solve for x+y
Look back in steps to see how I got this:
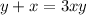
Divide both sides by 3

Original equation:
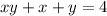
Substitute
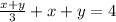
Multiply both sides by 3

Combine like terms:
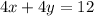
Divide both sides by 4
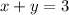
So now we finally arrive to our solution 3!!!!! I swear I felt like I was going in circles, and I was about to just stop trying to solve, because I had no idea what I was doing, sorry if I made some unnecessary intermediate steps.