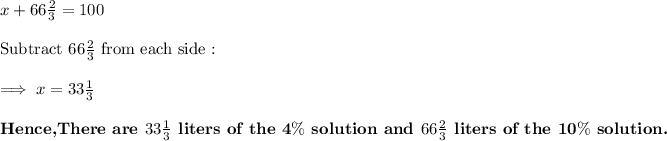Question

A 4% peroxide solution is mixed with a 10% peroxide solution, resulting in 100 L of an 8% solution. The table shows the amount of each solution used in the mixture. What is the value of z in the table?

Answer 1

its 8

Explanation:

100x0.08=8

plus i took the test on edg -_-

Answer 2

`\textbf{There are }33\tfrac{1}{3}\textbf{ liters of the 4}\%\textbf{ solution and }66\tfrac{2}{3}\textbf{ liters of the 10}\%\textbf{ solution.}`

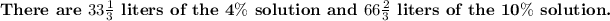
Explanation:

Let x represent the amount of 4% solution and y represent the amount of 10% solution.

⇒ x + y = 100 ..................(1)

x liters of the 4% solution gives us the expression 0.04·x

y liters of the 10% solution gives us the expression 0.10·y

100 L of the 8% solution gives us 0.08 × (100) = 8

⇒ 0.04·x + 0.10·y = 8 ...........(2)

This gives us the system of equations (1) and (2)

To solve this, we will use substitution.

Substituting x = 100 - y from equation (1) into equation (2). We get,

`y = 66\tfrac{2}{3}`

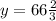
Substitute this value of y into the first equation:

`x + 66\tfrac{2}{3} = 100\\\\\text{Subtract }66\tfrac{2}{3}\text{ from each side :}\\\\\implies x = 33\tfrac{1}{3}\\\\\textbf{Hence,There are }33\tfrac{1}{3}\textbf{ liters of the 4}\%\textbf{ solution and }66\tfrac{2}{3}\textbf{ liters of the 10}\%\textbf{ solution.}`