Question

Suppose you roll a fair six sided die.Then you roll a fair eight sided die.Match each probability to it's correct value.

Answer 1

Explanation:

she's right

Answer 2

Case 1 matches with
`(5)/(48)`.

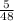Case 2 matches with
`(1)/(12)`.

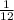Case 3 matches with
`(1)/(4)`.

Case 4 matches with
`(1)/(8)`.

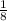Case 5 matches with
`(5)/(16)`.

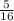Explanation:

We have a total sample space of six-sided die and an eight sided die.

(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8)

(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(2,7),(2,8)

(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(3,7),(3,8)

(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(4,7),(4,8)

(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(5,7),(5,8)

(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),(6,7),(6,8)

Case 1: The Probability that both numbers are odd numbers and their product is greater than 10. are: (3,5),(3,7),(5,3),(5,5),(5,7)

And total number of outcomes are: 48.

So, required probability is:
`(5)/(48)`.

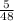Case 2: The probability that second number is twice the first number are:

(1,2),(2,4),(3,6),(4,8)

And total number of outcomes are: 48.

So, required probability is:
`(4)/(48)=(1)/(12)`.

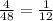Case 3: The probability of a number whose sum is multiple of 4 are:

(1,3),(1,7),(2,2),(2,6),(3,1),(3,5),(4,4),(4,8),(5,3),(5,7),(6,2),(6,6).

And total number of outcomes are: 48.

So, required probability is:
`(12)/(48)=(1)/(4)`.

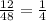Case 4: The probability that sum of two numbers is greater than 11.

(4,8),(5,8),(6,7),(6,8),(5,7),(6,6)

And total number of outcomes are: 48.

So, required probability is:
`(6)/(48)=(1)/(8)`.

Case 5:The probability that second number rolled is less than first number are:

(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5)

And total number of outcomes are: 48.

So, required probability is:
`(15)/(48)=(5)/(16)`.

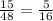So, the correct matches are:

Case 1 matches with
`(5)/(48)`.

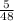Case 2 matches with
`(1)/(12)`.

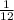Case 3 matches with
`(1)/(4)`.

Case 4 matches with
`(1)/(8)`.

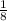Case 5 matches with
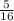`(5)/(16)`.