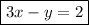Answer:
y = 3x - 2 slope-intercept
3x - y = 2 standard form
Explanation:
Parallel lines have the same slope.
The slope-intercept form of an equation of a line:

m - slope
b - y-intercept
We have the equation of a line in the standard form. Convert to the slope-intercept form:
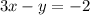 subtract 3x from both sides
subtract 3x from both sides
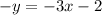 change the signs
change the signs
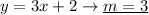
Therefore the slope-intercept form of the line is:
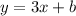
Put the coordinates of the point (2, 4) to the equation:
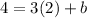
 subtract 6 from both sides
subtract 6 from both sides

Therefore:
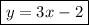 subtract 3x from both sides
subtract 3x from both sides
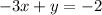 change the signs
change the signs