Answer:
As per the statement:
Elizabeth claims that the fourth root of 2 can be expressed as 2^m
"fourth root of 2" means
![\sqrt[4]{2} = 2^{(1)/(4)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/h9jlgx5g4d1mlne1xyeh3scrq0ilb6llcw.png)
then;
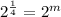
On comparing both sides we get;
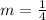
Since, it is also given:
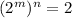
Solve for n;
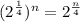
then;
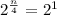
On comparing both sides we get;
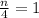
Multiply 4 both sides we get;
n = 4
Therefore, value of m and n are
 and 4
and 4