Question

Graph the system of inequalities . Which point represents a solution to the system?

Answer 1

Option B is correct.

(-4, -2)

Explanation:

Given the system of inequality:

-3x + 4y >0

x -3y >0

Option A:

(0, 0)

Substitute these point in the given system of equation.

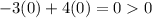`-3(0)+4(0) = 0> 0` False

0 -3(0) = 0 >0 False.

Option B

(-4, -2)

Substitute the value of point in the given system of equation.

-3(-4) + 4(-2) = 12 -8 = 4 >0 True

-4 -3(-2) = -4 +6 = 2 >0 True

Option C.

(6, 2)

Substitute the value of point in the given system of equation.

-3(6) + 4(2) = -18+8 = -10 >0 False

-6 -3(2) = -6 -6 = -12 >0 False

Option D

(6, 0)

Substitute the value of point in the given system of equation.

-3(6) + 4(0) = -18+0 = -18>0 False

-6 -3(0) = -6 -0 = -6 >0 False

Therefore, the only point which satisfies the given system of inequalities is, (-4, -2)