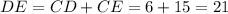Question

Charlene puts together two isosceles triangles so that they share a base, creating a kite. The legs of the triangles are 10 inches and 17 inches, respectively. If the length of the base for both triangles is 16 inches long, what is the length of the kite’s other diagonal? 6 inches inches inches 21 inches

Answer 1

Refer to the attached figure. We know that AB is 16 inches. We also know that AD=BD=10 and AE=BE=17

We're interested in DE, which we can compute as CD+CE

To compute CD, we can observe that ACD is a right triangle, and that AC is 8 inches long (it's half the base) and AD is 10 inches long (given).

So, by Pythagorean's theorem, we have

`CD = √(10^2-8^2) = √(36) = 6`

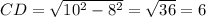
Similarly, we have

`CE = √(17^2-8^2) = √(225) = 15`

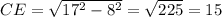
So, we have

`DE=CD+CE=6+15=21`

Answer 2

21 inches is the correct answer on edg.