Step-1) Simplifying the expression
Given expression:
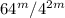
We can rewrite the expression (in the numerator and the denominator) as the product of multiple fours. Then, we can apply the exponent rule to simplify the expression to its simplest form. The simplest form will be the required simplified expression (solution to the provided expression).
We can apply the following exponent rule to simplify the expression:
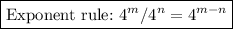
The exponent rule states that the "base" must be the same when subtracting exponents. If we divide a term with same bases, we can reduce work time by subtracting the exponent to simplify the expression.
Step-2) Equivalent or Non-equivalent?
Now, let us look at all the options to verify which term matches our simplified term, and which expressions do not match our simplified term.
First option:
Given term:
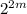
Can be re-written as:
Simplifying the expression inside the long brackets:
Therefore, the first option is equivalent to our simplified term.
Second option:
Given term:
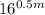
Can be re-written as:
Exponent Rule: (xᵃ)ᵇ = xᵃᵇ
Therefore, the second option is equivalent to our simplified term.
Third option:
Given term:
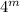
This term already matches our simplified term.
Therefore, the third option is equivalent to our simplified term.
Step-3) Conclude/verify your answer
We can conclude that all the options provided are equivalent to the given expression. We proved it by applying exponent rules and formulas.