Answer: The answer is 10 watermelons.
Step-by-step explanation: Given that Boris is going to buy pineapples and watermelons, a total of at least 16 fruits with $60 at most. The graph in the question represents the constraints on the number of pineapples P and watermelons W Boris buys.
From the graph, we have for condition A:
Two points are (16,0) and (0,16). So, the first constraint in equation form will be

And the constraint will be
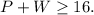
Also, from the graph, we have for condition B:
Two points are (20,0) and (0,15). So, the second constraint in equation form will be
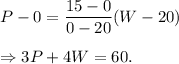
And the constraint will be
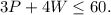
If Boris buy 6 pineapples, then from conditions A and B, we have
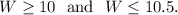
These will give us that W = 10.
Thus, Boris can buy 10 Watermelons to meet both his constraints.