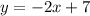ANSWER
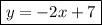
Step-by-step explanation
We want to write the equation in slope-intercept form for the line that passes through the point (3,2) and the intersection of the lines:

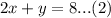
We subtract equation (1) from equation (2) to get,
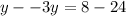
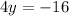
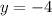
Put y=-4 into equation (2) to get the value of x.
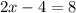

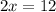
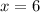
Therefore the line passes through (3,2) and
(6,-4).
The slope of this line is
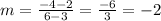
The slope intercept form is given by the formula,
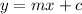
where m=-2 is the slope.
We substitute the slope to get,
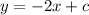
We substitute the point (3,2) to find the value of c.
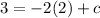
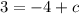
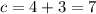
Hence the equation in slope-intercept form is