Answer:
The diagonals of the rhombus ABCD bisect each other
Explanation:
Given: ABCD is a rhombus and AC and BD are diagonals. All sides of the rhombus are equal.
To prove: AC and BD bisects each other.
Let O is the intersection point diagonals.
In triangle ABC, ABD, BCD and ADC are isosceles triangles.
In triangle AOB and COD,
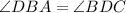
 (Vertically opposite angle)
(Vertically opposite angle)
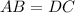 (opposite side of rhombus)
(opposite side of rhombus)
By AAS postulate,
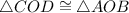
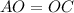 (CPCTC)
(CPCTC)
O is the midpoint of segment AC. Segment BD bisects segment AC.
In triangle AOD and COB,
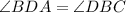
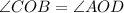 (Vertically opposite angle)
(Vertically opposite angle)
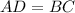 (opposite side of rhombus)
(opposite side of rhombus)
By AAS postulate,

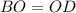 (CPCTC)
(CPCTC)
Segment BO is congruent to segment OD.
O is the midpoint of segment BD. Segment AC bisects segment BD.
Hence proved.