Question

PLEASE HELP!

All of the following are Pythagorean Identities EXCEPT:

A. sec^2(x) + 1 = tan^2(x)

B. 1 + cot^2(x) = csc^2(x)

C. sin^2(x) + cos^2(x) = 1

D. tan^2(x) + 1 = sec^2(x)

Answer 1

Only A is not Pythagorean Identity.

Explanation:

Let us draw a unit circle as shown in the attached figure.

In the given figure, let us apply Pythagorean theorem, which is given by

`x^2+y^2=z^2\\\\x=\sin\theta,y=\cos\theta,z=1\\\\\sin^2\theta+\cos^2\theta=1^2\\\\\sin^2\theta+\cos^2\theta=1........(C)`

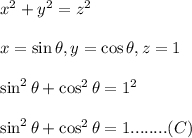
Divide both sides by
`\sin^2\theta`

`(\sin^2\theta)/(\sin^2\theta)+(\cos^2\theta)/(\sin^2\theta)=(1)/(\sin^2\theta)\\\\1+\cot^2\theta=\csc^2\theta.......(B)`

Divide both side of identity C by
`\sin^2\theta`

`(\sin^2\theta)/(\cos^2\theta)+(\cos^2\theta)/(\cos^2\theta)=(1)/(\cos^2\theta)\\\\\tan^2\theta+1=\sec^2\theta.......(D)`

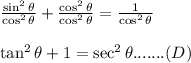
Therefore, only A is not Pythagorean Identity.