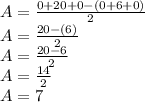Answer:
The perimeter is 13.213 units.
The area is 7 square units
Explanation:
O=(0,0)=(xo,yo)→xo=0, yo=0
A=(5,2)=(xa,ya)→xa=5, ya=2
B=(3,4)=(xb,yb)→xb=3, yb=4
Perimeter: P=OA+AB+OB
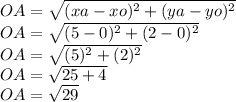
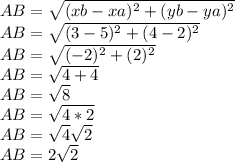
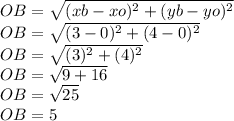
P=OA+AB+OB
P=√29+2√2+5
P=5.385+2(1.414)+5
P=5.385+2.828+5
P=13.213
Area: A
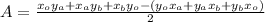
![A=((0)(2)+(5)(4)+(3)(0)-[(0)(5)+(2)(3)+(4)(0)] )/(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/o6grcvkqfgblo1awzj6c5my9xnai59i1m7.png)