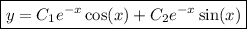Each of these ODEs is linear and homogeneous with constant coefficients, so we only need to find the roots to their respective characteristic equations.
(a) The characteristic equation for
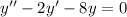
is
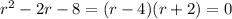
which arises from the ansatz
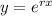 .
.
The characteristic roots are
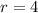 and
and
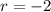 . Then the general solution is
. Then the general solution is
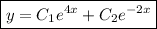
where
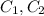 are arbitrary constants.
are arbitrary constants.
(b) The characteristic equation here is
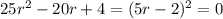
with a root at
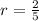 of multiplicity 2. Then the general solution is
of multiplicity 2. Then the general solution is
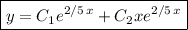
(c) The characteristic equation is
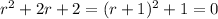
with roots at
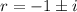 , where
, where
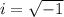 . Then the general solution is
. Then the general solution is
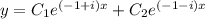
Recall Euler's identity,
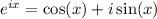
Then we can rewrite the solution as
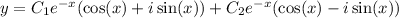
or even more simply as