Question

An archaeological team is excavating artifacts from a sunken merchant ship on the sea floor. To help with the exploration, the team is using a magnetic probe. The probe travels appropriately 3900 meters at an angle of depression of 67.4 degrees from the team’s ship on the ocean surface down to the ship on the ocean floor.

Complete the statements by filling them in with the missing measures rounded to the nearest meter.

1. When the probe reaches the ocean floor, the probe will be approximately _______ meters below the surface, measured vertically from the surface.

2. When the probe reaches the ocean floor, the horizontal distance of the probe from the team’s ship on the ocean surface will be approximately _______ meters.

Sorry for the blurry picture! If you could explain in detail, that would be great.

Answer 1

1). 3600 meters

2). 1499 meters

Explanation:

As we can see in the figure attached location of ship is at point S and probe is located at point B.

Part 1). we have to calculate the distance AB, vertically below the ocean surface.

In the ΔABS,

sin 67.4 =
`(AB)/(AS)`

0.9232 =
`(AB)/(3900)`

AB = 0.9232×3900

AB = 3600 meters

Part 2). In this part we have to calculate the horizontal distance BC of the probe from the team's ship on the ocean surface.

Since BC ≅ AS

Therefore, cos 67.4 =
`(AS)/(BS)`

0.3843 =
`(AS)/(3900)`

AS = 0.3843×3900 = 1498.75 ≈ 1499 meters

Answer 2

1) 1500 meters.

2) 3600 meters.

Explanation:

Firstly we need to find the value of angle x in the given figure attached to the answer and then use the trignometric identity to calculate the value for 1) and 2) part.

as we know that the triangle is a right angled triangle also second angle is given so we can find the value of the third triangle using the sum of all the angles of a triangle is 180°.

x+67.4°+90°=180°

x=22.6

1)

Now we know that:

`\sin x=(a)/(3900)\\\\\sin 22.6=(a)/(3900)\\\\0.3843=(a)/(3900)\\\\a=3900* 0.3843\\\\a=1498.77`

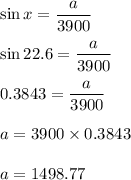
Hence to the nearest meter the value of a will be: a=1500 meter.

Hence, When the probe reaches the ocean floor, the probe will be approximately 1500 meters below the surface, measured vertically from the surface

2)

We are asked to find the value of 'b'.

As
`\cos x=(b)/(3900)\\\\\cos 22.6=(b)/(3900)\\\\0.9232=(b)/(3900)\\\\b=3900* 0.9232\\\\b=3600.48`

Hence to the nearest meter the value of b is 3600.

When the probe reaches the ocean floor, the horizontal distance of the probe from the team’s ship on the ocean surface will be approximately 3600 meters.