Question

if the feed per revolution on an upright drilling machine is set to 1/64" and the rpm is set to 105, how many revolutions are required for the drill to advance 2 1/8" into the part?

Answer 1

Proportion states that the two ratios or fractions are equal.

As per the given statement:

f the feed per revolution on an upright drilling machine is set to 1/64" and the rpm is set to 105.

Let x represents the revolutions are required for the drill to advance
`2(1)/(8)` into the part.

By definition of proportion:

`((1)/(64) )/(105) = ((17)/(8) )/(x)`

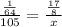
By cross multiply we have;

`(x)/(64)= 105 \cdot  (17)/(8)`

Multiply both sides by 64 we get;

`x = 105 \cdot 17 \cdot 8`

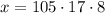
Simplify:

`x = 14,280`

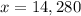
Therefore, 14,280 rpm revolutions are required for the drill to advance
`2(1)/(8)` into the part