Question

quadrilateral abcd is dilated to produce quadrilateral a′b′c′d′ with a scale factor of n. if the area of ABCD is r, what is the area of a’b’c’d’

Answer 1

The area of the quadrilateral a'b'c'd' is
`r(n^(2))\ units^(2)`

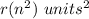
Explanation:

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z-----> the scale factor

x----> the area of the dilated quadrilateral a'b'c'd'

y----> the area of the original quadrilateral abcd

`z^(2)=(x)/(y)`

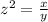
we have

`z=n`

`y=r\ units^(2)`

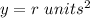
substitute the values

`n^(2)=(x)/(r)`

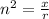
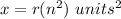`x=r(n^(2))\ units^(2)` ------> area of the quadrilateral a'b'c'd'