Using the "gradient, two-point form", we have:
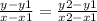
From the given data, we have that
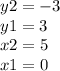
Therefore, substitute in the given values:
We have that:
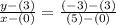
Simplify further
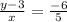
Multiply both sides by the LCM, 5x:
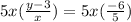
Simplify:
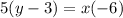
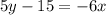
Note that the equation of a straight line is given by Ax + By = C where A and B are coefficients of x and y respectively. C is the constant. Hence:
6x+5y=15