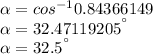Question

Find the angle between u=(8, -2) and v=(9,3) Round to the nearest tenth of a degree.

Answer 1

Short Answer. A) 32. 5

Explanation:

Edge 2021.

Answer 2

the angle between u=(8, -2) and v=(9,3) is 32.5°

Explanation:

u=(8,-2)=(u1,u2)→u1=8, u2=-2

v=(9,3)=(v1,v2)→v1=9, v2=3

We can find the angle between two vectors using the formula of dot product:

u . v =║u║║v║cos α (1)

And the dot product is:

u . v = u1 v1 + u2 v2

u . v = (8)(9)+(-2)(3)

u . v = 72-6

u . v = 66

║u║=√(u1²+u2²)

║u║=√((8)²+(-2)²)

║u║=√(64+4)

║u║=√(68)

║u║=√((4)(17))

║u║=√(4)√(17)

║u║=2√(17)

║v║=√(v1²+v2²)

║v║=√((9)²+(3)²)

║v║=√(81+9)

║v║=√(90)

║v║=√((9)(10))

║v║=√(9)√(10)

║v║=3√(10)

Replacing the known values in the formula of dot product (1):

u . v =║u║║v║cos α

66 = 2√(17) 3√(10) cos α

Multiplying:

66 = 6√((17)(10)) cos α

66 = 6√(170) cos α

Solving first for cos α: Dividing both sides of the equation by 6√(170):

`(66)/(6√(170) )=(6√(170)cos \alpha)/(6√(170) )`

`(66)/(6√(170))=cos\alpha`

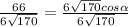
Simplifying: Dividing the numerator and denominator on the left side of the equation by 6:

(66/6)/(6√170/6)=cosα→11/√170=cosα→cosα=11/√170

cosα=11/13.03840481→cosα=0.84366149

`\alpha=cos^(-1)0.84366149\\\alpha=32.47119205^(\°)\\ \alpha=32.5^(\°)`