Answer:
x = -2
Explanation:
We are given the logarithmic base 2 equation of:
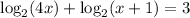
Apply logarithm property of addition where:
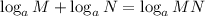
Therefore, we will write new equation as:
![\displaystyle{\log_2 [4x(x+1)] = 3}](https://img.qammunity.org/2023/formulas/mathematics/college/onaivu60jj5h27uo89a0xmrqennxolzy9c.png)
Apply logarithm to exponential form using:
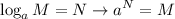
Thus, another new rewritten equation is:
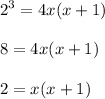
Expand the expression in and arrange the terms in quadratic expression:
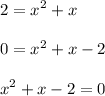
Solve for x:
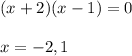
These are potential solutions to the equation. To find extraneous solution, you’ll have to know the domain of logarithm function. We know that logarithm’s domain is defined to be greater than 0. Henceforth, anti-logarithm must be greater than 0.
( 1 ) 4x > 0, x > 0
( 2 ) x + 1 > 0, x > -1
Therefore, our anti-log must be greater than 0, so any solutions that are equal or less than 0 will be considered as extraneous solution.
Hence, x = -2 is the extraneous solution.