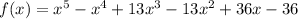Question

Write a polynomial function of least degree with integral coefficients that has the given zeros. 2i, 3i, 1

Answer 1

`f(x)=x^5-x^4+13x^3-13x^2+36x-36`

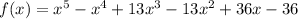
Explanation:

If the given zeros are 2i, 3i, and 1, the zeros of the function are: 2i, 3i, 1, -2i, and -3i, then the polynomial function is:

`f(x)=(x-2i)(x+2i)(x-3i)(x+3i)(x-1)`

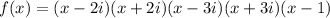
Using that the product of the difference and the sum is equal to the difference of the squares:

`(a-b)(a+b)=a^2-b^2`

`f(x)=(x^2-(2i)^2)(x^2-(3i)^2)(x-1)\\ f(x)=(x^2-2^2i^2)(x^2-3^2i^2)(x-1)\\ i^2=-1\\ f(x)=(x^2-4(-1))(x^2-9(-1))(x-1)\\ f(x)=(x^2+4)(x^2+9)(x-1)`

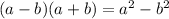
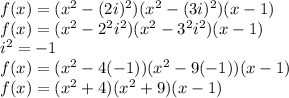
Multiplying the first and the second parentheses:

`f(x)=(x^4+(4+9)x^2+(4)(9))(x-1)\\ f(x)=(x^4+13x^2+36)(x-1)`

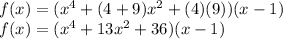
Multiplying the parentheses:

`f(x)=x(x^4)+x(13x^2)+x(36)-1(x^4)-1(13x^2)-1(36)\\ f(x)=x^5+13x^3+36x-x^4-13x^2-36`

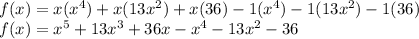
Ordering the terms:

`f(x)=x^5-x^4+13x^3-13x^2+36x-36`