Answer:
Explanation:
Let the width of the rectangular storage room be=x feet. Then, the length of the rectangular storage room is= (x+5) feet.
The area of the room =104 square feet
⇒
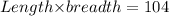
⇒
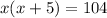
⇒
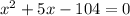
⇒
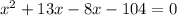
⇒
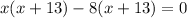
⇒
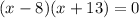
⇒x=8 and x=-13
Neglecting the negative value, we have the width of the rectangular storage room=x=8 feet.
Therefore, the length of the rectangular storage room=x+5=8+5=13 feet.
So, the dimensions of the room are 8 feet and 13 feet.