A designer increased the area of a tapestry by 20%. By what percent the width of tapestry was decreased in the process, if its length was increased by 50%?

Question

asked Feb 7, 2020 142k views

2 Answers

Glennanthonyb · Answer 1 · 2020-02-13T02:05:52+0000

Answer:

By 20% the width of tapestry was decreased in the process.

Explanation:

Given : A designer increased the area of a tapestry by 20% and length was increased by 50%?

To find : By what percent the width of tapestry was decreased in the process?

Solution : Let the length and width of the tapestry is l and w respectively.

So, The area of tapestry is
A=l* w

According to question,

A designer increased the area of a tapestry by 20%.

i.e, The new area is
$A_N= lw+20\% ( lw)$

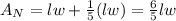
A_N= lw+(1)/(5) (lw)=(6)/(5)lw

And length was increased by 50%

i.e, The new length is
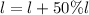
$l= l+50\% l$

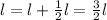
l= l+(1)/(2)l=(3)/(2)l

and let the new width is w'

Then the area is
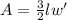
A=(3)/(2)lw'

So, to find the new width is

Area = New area

(3)/(2)lw'=(6)/(5)lw

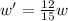
w'=(12)/(15)w

The percentage of width of tapestry decreased is

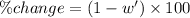
$\% change= (1-w')* 100$

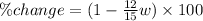
$\% change= (1-(12)/(15)w)* 100$

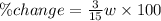
$\% change=(3)/(15)w* 100$

$\% change=20\%w$

Therefore, By 20% the width of tapestry was decreased in the process.