Question

Find the value of d.

Answer 1

First find the value or (DEA)
For this you will have to use the Pythagorean theory,

`{a}^(2) + {b}^(2) = {c}^(2)`
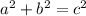
C is mainly the hypotenuse,
Meaning you either want to find A or B,

Since the hypotenuse has two segments, both values are 10, then just add them together making it 20,

Then 16 will be A or B, in this case it will be A,

To find a you must first move A to the other side by doing the opposite,

`{b}^(2) = {c}^(2) - {a}^(2)`
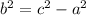
Now plug in the values,

`{b}^(2) = {20}^(2) - {16}^(2)`

`{b}^(2) = 400 - 256`

`{b}^(2) = 144`
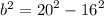
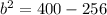
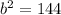
Now just find the square root of both factors,

`\sqrt{ {b}^(2) } = √(12)`
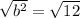
The value of (DEA) is,

`b = 12`
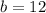
Now we want to find (d)
Since 12 is the value of the base, then divide it 2 to find (DE), after just repeat the whole process but with the value of hypotenuse 10 instead of 20 since we want to find the smaller triangle,

`{a}^(2) = {c}^(2) - {b}^(2)`
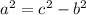
Now plug in the value

`{a}^(2) = {10}^(2) - {6}^(2)`

`{a}^(2) = 100 - 36`

`{a}^(2) = 64`
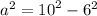
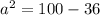
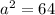
Now find the square root of both factors,

`\sqrt{ {a}^(2) } = √(64)`

`a = 8`

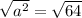
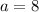
The value of (d) is (8)

Hope this helped
:D