Question

Suppose given △ABD and △CBD.

Suppose

AE

and

CE

are angle bisectors.

Prove that AD AB = DC CB .

Answer 1

The required result is proved with the help of angle bisector theorem.

Explanation:

Given △ABD and △CBD, AE and CE are the angle bisectors. we have to prove that
`(AD)/(AB)=(DC)/(CB)`

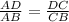
Angle bisector theorem states that an angle bisector of an angle of a Δ divides the opposite side in two segments that are proportional to the other two sides of triangle.

In ΔADB, AE is the angle bisector

∴ the ratio of the length of side DE to length BE is equal to the ratio of the line segment AD to the line segment AB.

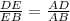`(DE)/(EB)=(AD)/(AB)` → (1)

In ΔDCB, CE is the angle bisector

∴ the ratio of the length of side DE to length BE is equal to the ratio of the line segment CD to the line segment CB.

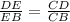`(DE)/(EB)=(CD)/(CB)` → (2)

From equation (1) and (2), we get

`(AD)/(AB)=(CD)/(CB)`

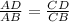
Hence Proved.