Question

PLEASE HELP!!!!!!!!

Calculate the pH for the following weak acid.

A solution of HCOOH has 0.19M HCOOH at equilibrium. The Ka for HCOOH is 1.8×10−4 . What is the pH of this solution at equilibrium?

Answer 1

Answer: 2.23

Step-by-step explanation:

The dissociation of acetic acid is as follows:

HCOOH(aq) ⇋ HCOO− (aq) + H+(aq)

The ICE table for the concentrations of ions is given below. From the table, the concentration of HCOO- and H+ can be found out.

HCOOH → HCOO− + H+
Initial Concentration 0.019 M 0 0
Equilibrium Concentration (0.019−x) M x x

Where,

• x is the concentration of the ions at equilibrium.

At equilibrium, dissociation constant can be calculated as follows.

`K_{\mathrm{a}}=\frac{x^(2)}{(0.19-x) \mathrm{M}}`

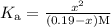
At equilibrium, the concentration of x is negligible as compared to that of HCOOH.

Substitute the value of Ka in the above equation.

`\begin{aligned}K_{\mathrm{a}} &=(x^(2))/(0.19-x) \\x &=\sqrt{1.8 * 10^(-4) * 0.19} \\&=0.00584 \mathrm{M}\end{aligned}`

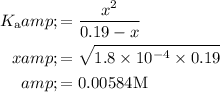
Here, the concentration of hydrogen ion is obtained. From the hydrogen ion concentration, the pH of the solution is found out as follows:

`\begin{aligned}\mathrm{pH} &=-\log \left[\mathrm{H}^(+)\right] \\&=-\log (0.00584 \mathrm{M}) \\&=2.23\end{aligned}`

Therefore, the pH of 0.19M HCCOH is 2.23