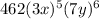Question

Find the seventh term of the expansion of

Answer 1

Correct choice is C

Explanation:

The i-th term of the binomial expansion
`\left(3x+7y\right)^(11)` is

`T_i=C^(11)_(i-1)\cdot \left(3x\right)^(11+1-i)\cdot (7y)^(i-1).`

If i=7, then

`T_7=C^(11)_(7-1)\cdot \left(3x\right)^(11+1-7)\cdot (7y)^(7-1)=C_6^(11)\cdot (3x)^5\cdot (7y)^6=462\cdot (3x)^5\cdot (7y)^6.`

Note that

`C_6^(11)=(11!)/(6!(11-6)!)=(6!\cdot 7\cdot 8\cdot 9\cdot 10\cdot 11)/(6!\cdot 1\cdot 2\cdot 3\cdot 4\cdot 5)=462.`

Answer 2

The correct answer option is C.
`462 (3x)^5 (7y)^6`.

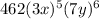Explanation:

We are given the following expression to be expanded and we are to find its seventh term:

`(3x+7y)^(11)`

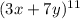
The coefficient here is taken from Pascal's triangle (nCr on the calculator).

The expression expands in a way such that, the power of the first term decreases by one each time while it increases for the second term.

1st term:
`1 (3x)^11`

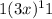
2nd term:
`11 (3x)^(10) (7y)^1`

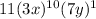
3rd term:
`55 (3x)^9 (7y)^2` and so on.

Therefore, the 7th term will be
`462 (3x)^5 (7y)^6`