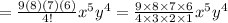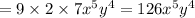Question

Find the 5th term of the expansion of (x + y)^9

a.
81x4y5
c.
81x5y4
b.
126x4y5
d.
126x5y4


Please select the best answer from the choices provided

A
B
C
D

Answer 1

Option d.
`126x^5y^4`.

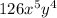Explanation:

Based on binomial theorem we write down the binomial formula for all positive integer values of n as-

`(a+b)^(n)=a^(n)+na^(n-1)b+(n(n-1))/(2!)a^(n-2)b^(2)+(n(n-1)(n-2))/(3!)a^(n-3)b^(3).....b^(n)`

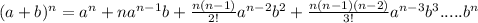
Now we calculate the 5th term of
`(x+y)^(n)`

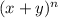
From the given formula the fifth term of the binomial will be

=
`(n(n-1)(n-2)(n-3))/(4!)x^(n-4)y^(4)`

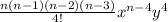
Here the value of n = 9

Then the fifth term will be
`=(9(9-1)(9-2)(9-3))/(4!)x^(9-4)y^(4)`

`=(9(8)(7)(6))/(4!)x^(5)y^(4)=(9* 8* 7* 6)/(4* 3* 2* 1)x^5y^4`

`=9* 2* 7x^5y^4=126x^5y^4`