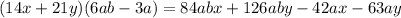Answer:
Explanation:
Given : Two expression
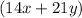 and
and
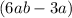
To write : A product of 2 binomials and a monomial of the given expression
Solution :
To find the product of the given expression we have to first open the parenthesis and after opening we have to multiply each term of first expression with each term of another expression to get the result.
Step 1 - Write as a product
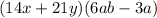
Step 2- Multiply term by term
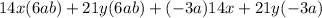
Step 3- Solve the expression
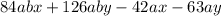
Therefore, The required product is