Answer:
this result can approximate 0.34Kcal/kg.ºC
Step-by-step explanation:
As during the process the material only changes its temperature we use the sensible heat formula
sensible heat formula
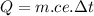
Data
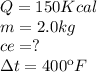
The options given to us by the unit of temperature is celsius, so we must transform from F to celsius
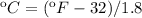
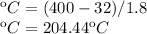
Now we clear the specific heat of the sensible heat formula
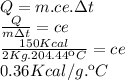
this result can approximate 0.34Kcal/kg.ºC