Question

In triangle △ABC, ∠ABC=90°, BH is an altitude. Find the missing lengths. AH=HC+2 and BC=2, find HC.

Answer 1

The measure of HC is 1 unit.

Explanation:

Given,

In triangle ABC,

∠ABC = 90°, BC = 2,

Also, H∈ AC such that ∠BHC = 90°,

And, AH = HC + 2

We have to find : HC

∵ ∠ABC = ∠BHC ( right angles )

∠ACB = ∠HCB

By the AA similarity postulate,

`\triangle ABC\sim \triangle BHC`

∵ The corresponding sides of similar triangles are in same proportion,

`\implies (BC)/(HC)=(AC)/(BC)`

`(2)/(HC)=(AH+HC)/(2)`

`4=HC(HC+2+HC)`

`4=HC(2HC+2)`

`4=2HC(HC+1)`

`2=HC(HC+1)`

`\implies HC^2+HC-2=0`

`HC^2+2HC-HC-2=0`

`HC(HC+2)-1(HC+2)=0`

`(HC+2)(HC-1)=0`

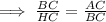
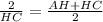
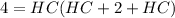
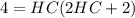
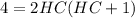
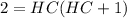
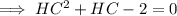
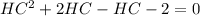
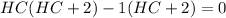
By zero product property,

HC = -2 ( not possible ) or HC = 1

Hence, the measure of HC is 1 unit.

Answer 2

HC = 1

Explanation:

AC = HC +AH = HC +(HC+2) = 2·HC +2

The altitude divides the triangle into similar triangles, so the ratio of hypotenuse to short side is the same for all. That is ...

BC/HC = AC/BC

2/HC = (2HC +2)/2

4 = 2(HC)(HC +1) . . . . . cross multiply

0 = HC² +HC -2 . . . . . . divide by 2, subtract 2

0 = (HC -1)(HC +2) . . . . factor. Solutions are those values of HC that make the factors be zero.

The useful solution is ...

HC = 1