Answer:
The first three terms of the series are 8, 10 and 12. The number of terms is 12 to make the sum 228.
Explanation:
The series is defined as
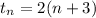
Put n=1.
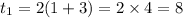
Put n=2.
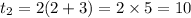
Put n=3.
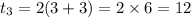
The first three terms of the series are 8, 10 and 12.
It is an arithmetic series. The first terms is 8 and the common difference is
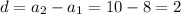
The sum of n terms of an arithmetic series is
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/high-school/p82o14tt1akmx6szgemiszk1cohd2h7amw.png)
![288=(n)/(2)[2(8)+(n-1)2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/m9zkmelr17pj8zqvmhhz8a8jb14r3d4tfc.png)
![288=(2n)/(2)[8+n-1]](https://img.qammunity.org/2020/formulas/mathematics/high-school/rcr8z62dg4ekhvv1e0v2d1312dc1rxpsad.png)
![288=n[n+7]](https://img.qammunity.org/2020/formulas/mathematics/high-school/cysb0ew7yhjvpdhuil0hksiad2y1tguobq.png)
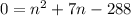
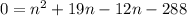
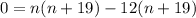

Equate each factor equal to zero.
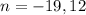
The number of terms can not be negative, therefore the value of n must be 12.