Question

When simplifying a^2+3a over a^3-2a^2-15a, what are the term(s) that can be cancelled

Answer 1

a and (a+3)

Explanation:

We have the following expression and we will simplify it and see which terms can be cancelled out:

`\frac {a^2 + 3a} { a^3 - 2a^2 - 15a }`

Now factoring both the numerator and the denominator to get the like terms which can then be cancelled out.

`\frac {a^2 + 3a} {a^3 - 2a^2 - 15a } = \frac { a ( a + 3 ) }{a ( a - 5 )( a + 3 )}`

`a` and
`(a+3)` are the common terms so they are cancelled and we are left with
`(1)/((a-5))`.

Answer 2

a(a+3) are the terms which can be cancelled.

Explanation:

In this question if we factorize both the expressions then we can get the common factors which can be cancelled.

So first we factorize a²+3a = a( a+3 )

Now the second expression
`a^(3)-2a^(2)-15a`

⇒
`a(a^(2)-2a-15)`

⇒
`a(a^(2)-5a+3a-15)`

⇒
`a\left \{ a(a-5))+3(a-5)) \right \}`

⇒
`a(a+3)(a-5)`

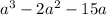
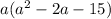
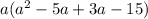
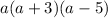
Now it is clear to us that factors a(a+3) are the common factors that can be cancelled.